
Plakatowanie (pla)
Pomóż nam usprawnić bazę zadań!
Postering
Memory limit: 32 MB
All the buildings in the east district of Byteburg were built in accordance with the old arbitecture: they stand next to each other with no spacing inbetween. Together they form a very long chain of buildings of diverse height, extending from east to west.
The mayor of Byteburg, Byteasar, has decided to have the north face of the chain covered with posters. Byteasar ponders over the minimum number of posters sufficient to cover the whole north face. The posters have rectangular shape with vertical and horizontal sides. They cannot overlap, but may touch each other, i.e. have common points on the sides. Every poster has to entirely adjoin the walls of certain buildings and the whole surface of the north face has to be covered.
Task
Write a programme that:
- reads the description of buildings from the standard input,
- determines the minimum number of posters needed to entirely cover their north faces,
- writes out the outcome to the standard output.
Input
The first line of the standard input contains one integer  (
(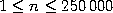 ), denoting the number of buildings the chain
comprises of.
Each of the following
), denoting the number of buildings the chain
comprises of.
Each of the following  lines contains two integers
lines contains two integers 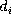 and
and 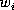 (
(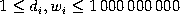 ),
separated by a single space, denoting respectively the length and height
of the
),
separated by a single space, denoting respectively the length and height
of the  building in the row.
building in the row.
Output
The first and only line of the standard output should contain one integer, the minimum number of rectangular posters that suffice to cover the north faces of the buildings.
Example
For the input data:
5 1 2 1 3 2 2 2 5 1 4
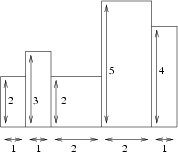
the correct result is:
4

The figures show the north face of the buildings chain. The second figure shows an exemplary covering of the face with four posters.
Task author: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English